Couple rendement risque bourse

Les multiples recherches en économie et en finance ont mis à jour les concepts de marchés « efficients ». Les marchés financiers et plus particulièrement le marché des actions sont soumis aux influences des informations passées et aux anticipations  futures.

La valorisation des titres ne serait alors que le reflet des informations arrivant sur le marché conduisant à la valorisation de celui-ci qui ne serait qu’un « miroir parfait » de la réalité.

Les crises financières des années précédentes remettent en cause la théorie de l’efficience des marchée et de l’existence de la symétrie avec  l’information.

Le couple rendement risque :

Lorsqu’un investisseur est positionné sur un actif, il peut à tout moment calculer le rendement obtenu en intégrant les revenus perçus pendant la période de détention, les plus values réalisées et la valorisation sur le marché.

Il ne peut au moment de l’achat anticiper les revenus à venir ni le potentiel de valorisation. Il est donc en risque.

Le rendement d’une action est déterminé par la variation relative des cours entre deux dates, à laquelle viennent s’ajouter les dividendes distribués.

Cette observation peut être effectuée sur une période hebdomadaire, mensuelle ou annuelle dont la série statistique des rendements permet de déterminer le risque, par le calcul de l’écart-type. Ce calcul devient alors un déterminant de la volatilité historique.

Cette analyse comparative permet de mettre en évidence la dispersion des points obtenus par rapport au rendement de référence moyen. C’est également un outil permettant de déterminer une hiérarchie au sein des diverses classes d’actifs.

Le risque de marché et le risque spécifique :

Les qualités intrinsèques des entreprises sont déterminées au travers de leur analyse fondamentale. Cette appréciation ne peut occulter la visibilité économique du contexte général du marché. Il existe alors une interdépendance entre le rendement d’une action et son indice de référence. (ex : CAC40) qui peut être mise en évidence par une analyse des données.

Une recherche de données de rendements mensuels sur l’action et l’indice s’avère nécessaire pour représenter chaque couple (rendement mensuel de l’action, rendement mensuel de l’indice) par un point afin de constituer un nuage de points par lequel viendra s’insérer une droite de régression.

Le « modèle de marché » ainsi représenté établit un lien statistique entre le rendement de l’action et celui de l’indice de référence qui s’exprime de la manière suivante :

Rendement de l’action = α + β x rendement marché (indice) + ε

α = alpha : intersection de la droite de régression avec l’axe des ordonnées

β = bêta : pente de la droite de régression

ε = variable aléatoire résiduelle

Interprétation et utilisation des coefficients α, β, ε

• α  est le rendement de l’action qui serait obtenu si le rendement de marché était nul.
• β indique le lien statistique entre les variations (rendements) de l’action et celle de l’indice.
• Une variation de 1% de l’indice (marché) laisse entendre une variation de β% de l’action.
• Un β>1 indique que l’action amplifie l’évolution de l’indice de référence.
• Un β<1 indique que l’action amorti les variations de l’indice de référence, on parle alors d’action défensive.
• L’écart-type de la variable aléatoire ε constitue la mesure du risque spécifique à l’action.

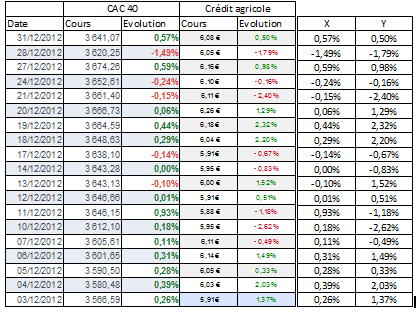
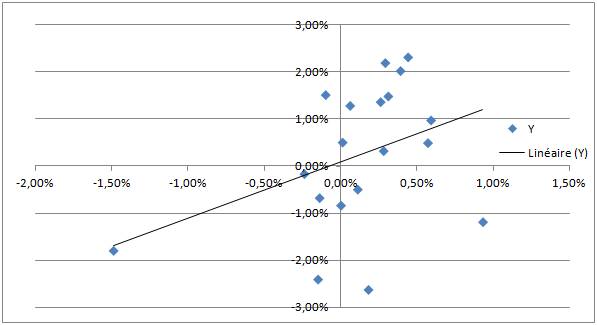
La droite de régression donne les indications suivantes :

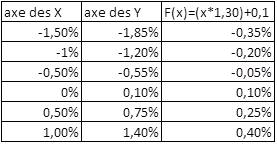
• Si « α »  est le rendement de l’action qui serait obtenu si le rendement de marché était nul, dans ce cas, nous obtenons 0.10% d’évolution de l’action en cas de stabilité du marché.
• Le « β » est de 1.30 indique le lien statistique entre les variations (rendements) de l’action et celle de l’indice, il indique que l’action amplifie l’évolution de l’indice de référence.
• Quand le CAC40 monte de 1%, l’action monte de 1.40%
• Quand le CAC40 baisse de 1%, l’action baisse de 1.20%