Calcul de la VaR

La mesure du risque financier lié à la constitution d’un portefeuille est aujourd’hui une notion incontournable auxquels les gestionnaires doivent faire face. Les accords de Bâle II en 1997 préconisent l’usage de l’approche VaR pour mesurer le risque de marché. 

Historique des approches du risque : 

1954 : Harry Markowitz introduit la notion de diversification (couple rendement/risque), et une sélection de titres basée sur l’écart type par rapport à un portefeuille efficient. 

1964 : William Sharpe propose le modèle CAPM (Capital Asset Pricing Model) approche risque de marché. 

1976 : Stephen Ross présente une approche multidimensionnelle du risque avec le modèle MEA (Arbitrage Pricing Theory).

1993 : JP Morgan propose l’approche de la VaR. Elle représente la perte potentielle maximale d’un investisseur sur la valeur d’un actif, ou d’un portefeuille d’actifs financiers, compte tenu d’un horizon de détention et d’un intervalle de confiance.

Il existe trois méthodes de calcul de VaR :

La méthode paramétrique, la méthode historique, la méthode Monte-Carlo.

Exemple d’exercice Méthode des historiques :

Nous baserons notre étude sur la base du rapatriement des 500 dernières valeurs de clôture quotidiennes du CAC40 et nous calculerons les gains quotidiens journaliers qui seront triés par valeur.

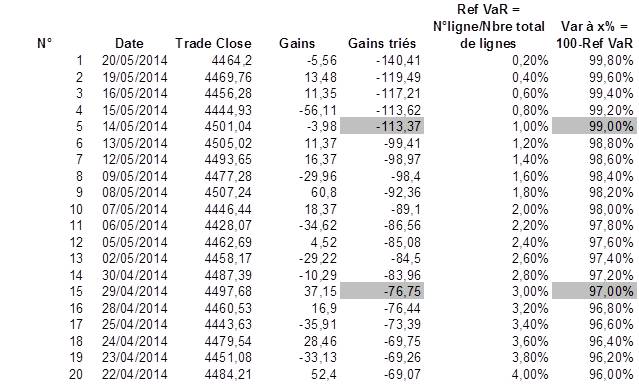
Calcul de la VaR à 99% et à 1 jour :

Ainsi, la VaR (99%, 1jour) = -113.37€ soit 2.51% (-113.37€/4501.04€) 

Calcul de la VaR à 97% et à 1 jour :

Ainsi, la VaR (97%, 1jour) = -76.75€ 

On obtient la VaR à 10 jours par transcription de la VaR à 1 jour en multipliant la VaR à 1 jour par la racine carré de la durée, soit :

Var (99%, 10 jours) = -113.37€ * √10 = -358.50€

Var (97%, 10 jours) =   -76.75€ * √10 = -242.70€ 

La valeur de la VaR à 10 jours nous indique que sur une période de 10 jours, il n’y a que :

• 1% de chance que la perte dépasse les 358.50€ pour une VaR à 99%
• 3% de chance que la perte dépasse les 242.70€ pour une VaR à 97% 

Exemple d’exercice Méthode des paramétrique :

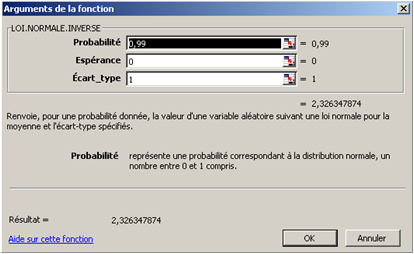
=LOI.NORMALE.INVERSE (0,99;0;1)

= 2.33%

Le coefficient de 2.33% correspond à l’écart maximum attendu pour une VaR à 99% et à 1 jour.

Bien que très proche du résultat initial, celui-ci est issu d’une méthode paramétrique implantée dans Excel qui ne peut être un reflet plus exact que la méthode manuelle.

La Méthode de Monte Carlo :

Elle fait appel à la génération de nombres aléatoires qui peuvent être obtenus grâce à des algorithmes mathématiques implantées sur une loi gaussienne.

Le modèle Black&Scholes fait référence en la matière.