Evaluation d'une entreprise
Variance, Covariance et Bêta
La Variance :
En statistique et en théorie des probabilités, la variance est une mesure de la dispersion des valeurs d'un échantillon ou d'une distribution de probabilité.
La variance est la différence entre la moyenne des carrés et le carré de la moyenne.
.
.
La Covariance :
En théorie des probabilités et en statistique, la covariance entre deux variables aléatoires est un nombre permettant de quantifier leurs écarts conjoints par rapport à leurs espérances respectives.
Interpétration : Si une valeur de covariance, quel que soit par ailleurs son signe, positif ou négatif, est élevée, vous pourrez en que les deux éléments rapprochés sont fortement corrélés, que ce soit positivement ou négativement.
![\operatorname {Cov}(X,Y)\equiv \operatorname {E}[(X-\operatorname {E}[X])\,(Y-\operatorname {E}[Y])]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2bcb5b8b1cacb90025fc0b1a4577c43a649d0bd)
Bêta :
Le Bêta (β) est un coefficient de corrélation entre un un actif et le marché.
Il est utilisé comme mesure de volatilité.
- Si le bêta d’une action par rapport à son indice est supérieur à 1, alors la volatilité de cette action est généralement supérieure à son indice.
- Si le bêta est au contraire inférieur à 1, alors la volatilité de cette action est inférieure à son indice ou l’action est volatile mais peu corrélée au marché.
Le bêta représente finalement le risque non diversifiable d’un actif, autrement dit, son risque systématique (par opposition au risque idiosyncratique).
Exercice :
- Calculez la Variance, Covariance et Bêta pour les données suivantes.
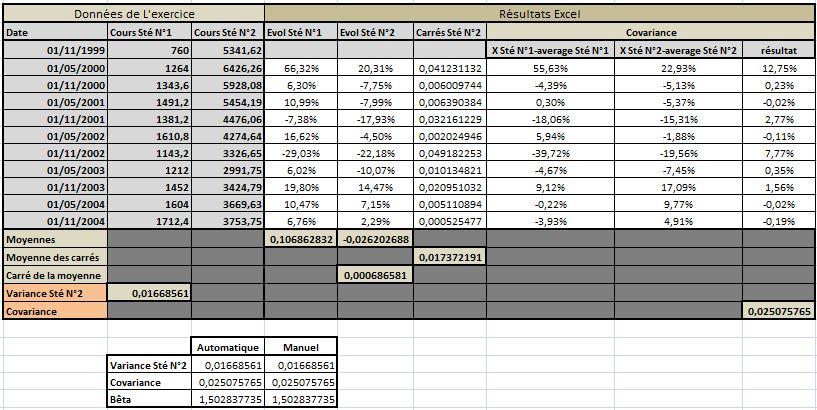
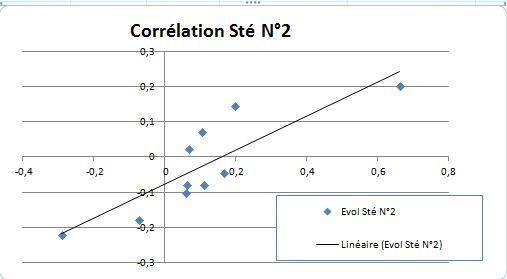
Calcul de la relation MEDAF
Relation du MEDAF :
Le modèle d'évaluation des actifs financiers (MEDAF),vient de l'anglais Capital Asset Pricing Model (CAPM).
Le coût des capitaux propres correspond au taux de rendement requis des actionnaires d'une entreprise eu égard à la rémunération qu'ils pourraient obtenir d'un placement présentant le même profil de risque sur le marché.
Selon ce modèle, le taux de rentabilité d’un actif est égale au taux de l’actif sans risque "taux des OAT à 10 ans" par exemple auquel s’ajoute une prime de risque et décrit la relation entre le risque d'un actif financier et la rentabilité espérée de cet actif.
Formule du MEDAF : (Coût des capitaux propres)
E(rj) =Rf + Bactif. [E(rm) - Rf]. E(ractif ) = rentabilité attendue
| Coût des fonds propres Calcul de l'Espérence de rentabilité du titre |
|
| E(rm) = espérence de rentabilité du marché | 8,50% |
| Rf : Cout de l'actif sans risque (OAT 10 ans par exemple) | 5,50% |
| βj = covariance (Rj,Rm)/Variance(Rm) : Bêta | 1,502837735 |
| E(rj) : Espérence de rentabilité du titre | 10,01% |
Modèle Gordon-Shapiro
Le modèle Gordon Shapiro ou DDM (dividend discount modela) été mis au point en 1956.
C'est un modèle d'actualisation des actions particulièrement connu.
Mis au point par Myron J. Gordon et Eli Shapiro, ce modèle, dit aussi de "croissance perpétuelle", ne tient pas compte des plus-values, et considère que lorsque le flux de dividendes est perpétuel (c'est à dire qu'il tend vers l'infini), la plus value n'a pas d'incidence sur l'évaluation de l'action.
Formule Gordon Shapiro :
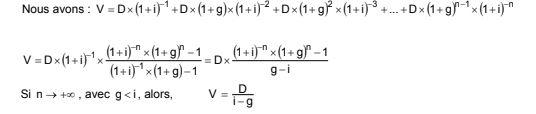
De cette suite géométrique, nous obtenons la formule Gordon Shapiro : V = D/(i-g)
Télécharger la feuille Excel :
| Evaluation à partir des dividendes futurs | |
|
D1 : Dividende unitaire prévu pour la période N+1 (avoir fiscal compris ou non) |
15,00 |
| i : cout des fonds propres | 10,01% |
| g : Taux de croissance des dividendes avec G < I | 3% |
| V : valeur de l'action (Formule) Gordon Shapiro | 214,03 |
| Nombre d'actions | 600 000,00 |
| Valeur de l'entreprise | 128 415 253,4 |
Gordon Shapiro https://boursegestionportefeuille.e-monsite.com
Date de dernière mise à jour : 2025-02-01
Français
English
